1 Motivation

Here we explore the data from 2015 season. 2015 was chosen arbitrarily among recent years. There's a few reasons for visualizing a single season at a time.

  • It keeps the code simple. We can later write functions to do the same for the other seasons or multiple seasons combined.

  • It reflects my general modeling approach: Stay simple until there are reasons not to.

    Our main goal is to predict the outcomes of the 2019 tournament. Regular season results from 2019 season might help us with this prediction, but it's not clear what information can be gained from previous seasons, given that the roster goes through a significant change each season. For instance, what can we actually learn from the 2000 season that can help us predict the outcomes of the 2019 tournament? Not that useful information can't be shared across seasons, but we'll explore the incremental benefits of using larger datasets and more complicated models.

    Focusing on a single season at a time helps us retain simplicity and interpretability. The goal, of course, is to expand our models, and we'll do that in a way that helps us gain insight about the problem domain.

2 Setup

2.1 Load Packages

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
from tabulate import tabulate
from src import utils  # see src/ folder in project repo
from src.data import make_dataset

2.2 Helper Functions

print_df = utils.create_print_df_fcn(tablefmt='html');
show_fig = utils.create_show_fig_fcn(img_dir='eda/eda_2015/');

2.3 Load Data

data = make_dataset.get_train_data_v1(season=2015)
# difference in scores
data['scorediff'] = data['score1'] - data['score2']
# winning and losing scores
data['score_w'] = np.where(data.team1win == 1, data.score1, data.score2)
data['score_l'] = np.where(data.team1win == 0, data.score1, data.score2)
print('Data size = {}'.format(data.shape))
print_df(data.head())
Data size = (5421, 19)
season daynum numot tourney team1 team2 score1 score2 loc team1winseed1 seednum1 seed2 seednum2 seeddiff ID scorediff score_w score_l
0 2015 11 0 0 1103 1420 74 57 1103 1nan nan nan nan nan2015_1103_1420 17 74 57
1 2015 11 0 0 1104 1406 82 54 1104 1nan nan nan nan nan2015_1104_1406 28 82 54
2 2015 11 0 0 1112 1291 78 55 1112 1Z02 2 nan nan nan2015_1112_1291 23 78 55
3 2015 11 0 0 1113 1152 86 50 1113 1nan nan nan nan nan2015_1113_1152 36 86 50
4 2015 11 0 0 1102 1119 78 84 1119 0nan nan nan nan nan2015_1102_1119 -6 84 78

2.4 Basic Description

n_missing = data.isna().sum().rename('n_missing')
print_df(data.describe().append(n_missing))
season daynum numot tourney team1 team2 score1 score2 team1win seednum1 seednum2 seeddiff scorediff score_w score_l ID loc seed1 seed2
count 54215421 5421 5421 5421 5421 5421 5421 5421 1166 1161 376 5421 5421 5421 nan nan nan nan
mean 2015 71.5853 0.0791367 0.01235931224.32 1343.95 66.3785 67.3331 0.472607 8.57719 8.62532 0.361702 -0.954621 72.6838 61.0279 nan nan nan nan
std 0 36.0027 0.326858 0.110494 85.1581 84.8386 12.0862 11.9573 0.499295 4.77696 4.60865 5.70773 14.6983 10.541 10.5097 nan nan nan nan
min 2015 11 0 0 1101 1106 26 26 0 1 1 -15 -62 38 26 nan nan nan nan
25% 2015 40 0 0 1154 1285 58 59 0 4 5 -3 -10 65 54 nan nan nan nan
50% 2015 74 0 0 1210 1359 66 67 0 9 9 0 -2 72 61 nan nan nan nan
75% 2015 103 0 0 1281 1414 74 75 1 13 12 4 9 79 68 nan nan nan nan
max 2015 154 4 1 1460 1464 116 126 1 16 16 15 69 126 111 nan nan nan nan
n_missing 0 0 0 0 0 0 0 0 0 4255 4260 5045 0 0 0 0 0 4255 4260

3 Visualizations

3.1 Distribution of points from each team

fig, axes = plt.subplots(2, 2, figsize=(8, 8), sharex=True, sharey=True)
for i, (is_tourney, df) in enumerate(data.groupby('tourney')):
    color = '#1f77b4' if is_tourney == 0 else '#ff7f0e'
    axes[i,0].scatter(df.score1, df.score2, s=1, c=color)
    axes[i,1].hexbin(df.score1, df.score2, bins='log', gridsize=50)
    lims = [20, 125]
    axes[i,0].set_ylabel('Team 2 Score ({})'.format('Regular' if is_tourney == 0 else 'Tourney'))
    axes[i,1].set_xlim(lims)
    axes[i,1].set_ylim(lims)
    for j in range(2):
      axes[i,j].plot(lims, lims, c='r', lw=0.5)
axes[1,0].set_xlabel('Team 1 Score')
axes[1,1].set_xlabel('Team 1 Score')
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.05, hspace=0.05)
plt.suptitle('Bivariate Distribution of Points')
show_fig('scatter_points.png')

scatter_points.png

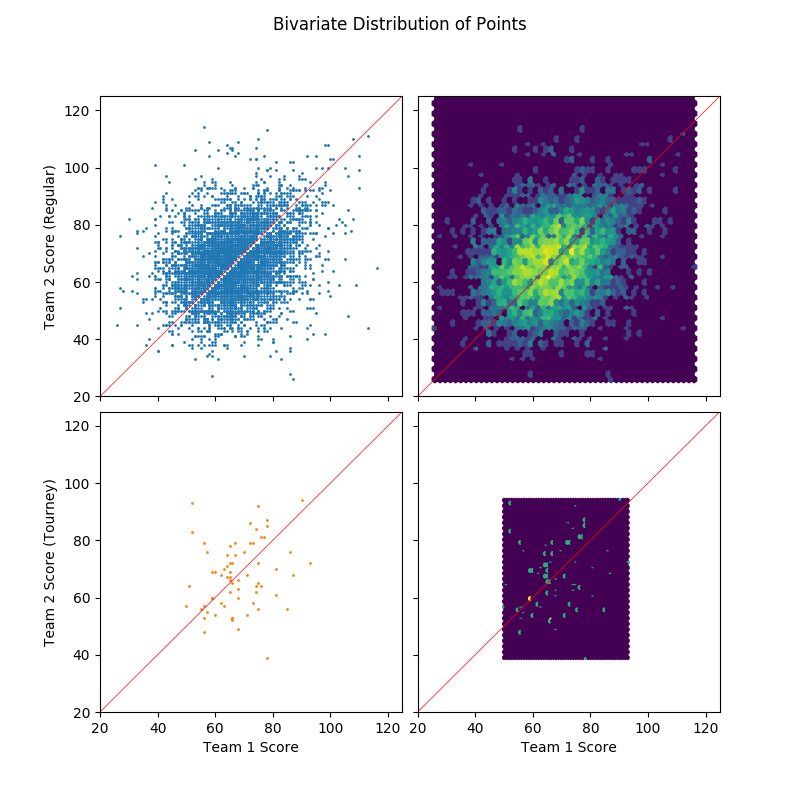
An initial look at the distribution of points scored by team 1 (with lower ID) and team 2 (with higher ID). As expected, there's nothing special here which means that team IDs are probably assigned arbitrarily.

3.2 Proportion of win by difference in seeds

df_tmp = data.groupby(['tourney', 'seeddiff'])['team1win'].agg(['sum', 'size']).reset_index()
fig, axes = plt.subplots(2, 1, figsize = (7, 10), sharex=True)
for i, (is_tourney, df) in enumerate(df_tmp.groupby('tourney')):
    axes[i].bar(df.seeddiff, df['size'], label='Loss')
    axes[i].bar(df.seeddiff, df['sum'], label='Win')
    axes[i].set_title('Regular' if is_tourney == 0 else 'Tourney')
axes[1].set_xlabel('Difference in Seeds')
handles, labels = axes[0].get_legend_handles_labels()
fig.legend(handles, labels, loc='right')
show_fig('bar_win_by_seeddiff.png')

bar_win_by_seeddiff.png

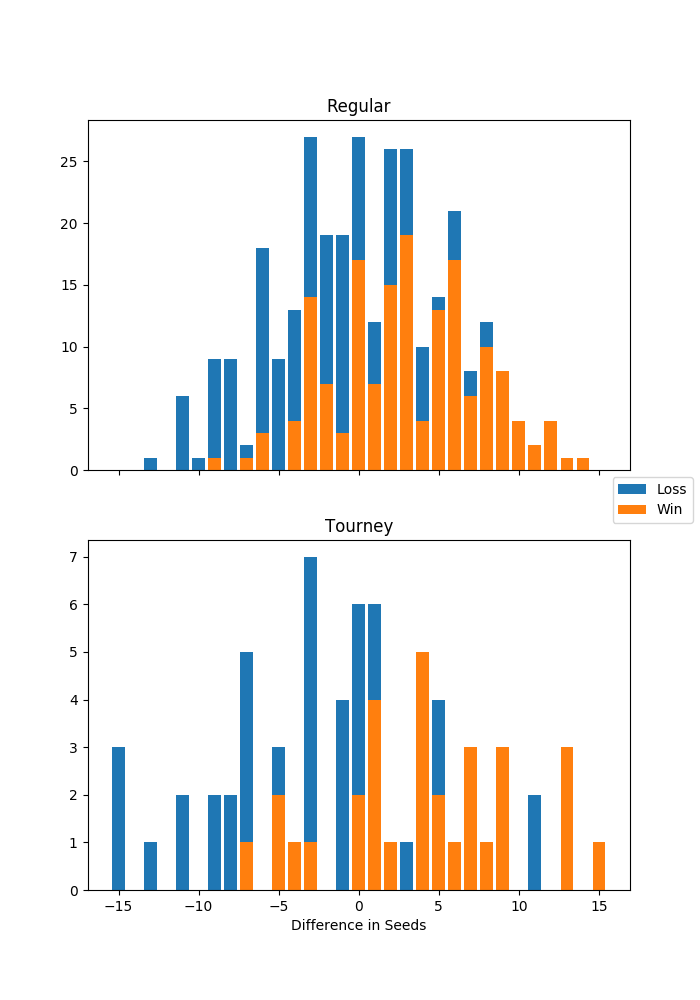
This figure shows the result of the games between seeded teams. Win, loss, and difference in seeds are from the perspective of team 1, or the team with the lower ID. For example, there were 3 tournament games in which team 1 was the underdog by 15 seed points, and all resulted in a loss. There were also two upsets in the tournament in which teams who had 11 seed point advantage lost the game.

3.3 Difference in scores by difference in seeds

sns.lmplot(x='seeddiff', y='scorediff', hue='tourney', data=data, aspect=1.5)
show_fig('scatter_scorediff_by_seeddiff.png')

scatter_scorediff_by_seeddiff.png

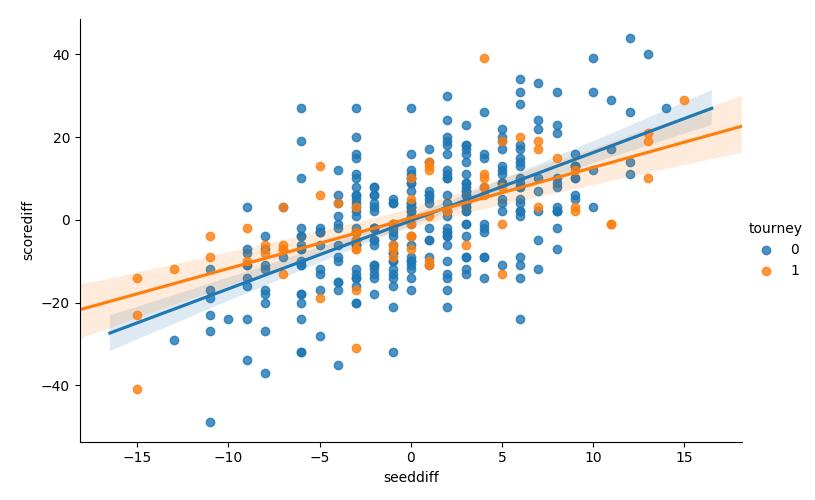
There isn't a huge difference, but the slope between scorediff and seeddiff is less steep for the tournament games. This means that the games tend to be closer in the tournament than regular season, controlling for the difference in seeds. The difference in slopes might be used to quantify the increase in competitiveness in the tournament.

3.4 Win vs. difference in seeds

sns.lmplot(x='seeddiff', y='team1win', hue='tourney', data=data,
           scatter_kws={"s": 5}, y_jitter=0.03, logistic=True, aspect=1.5)
show_fig('scatter_win_by_seeddiff.png')

scatter_win_by_seeddiff.png

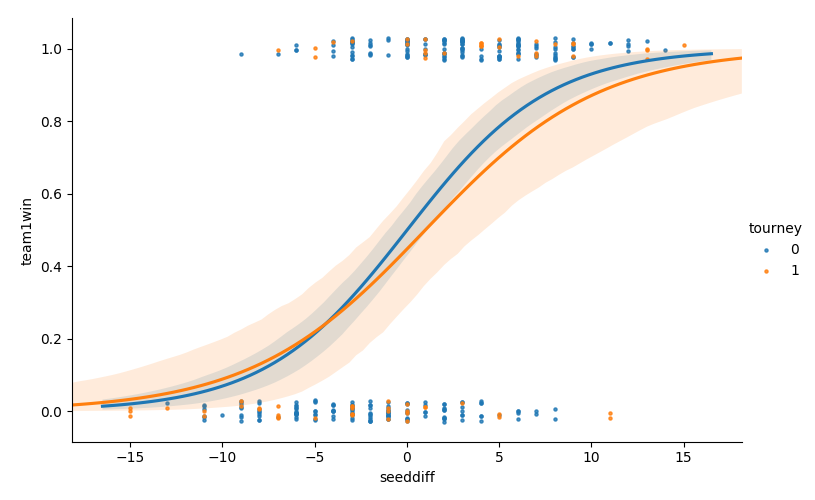
Similar result here as above, but for the logistic regression curve. The difference in seeds has less impact on the winning probabilities in the tournament than during regular season.

3.5 Distribution of winning vs. losing points

fig, axes = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(10, 6))
axes[0].scatter(data['score_l'], data['score_w'], s=1)
axes[1].hexbin(data['score_l'], data['score_w'], bins='log', gridsize=50)
plt.subplots_adjust(left=0.1, bottom=0.2, right=None, top=None, wspace=0.05, hspace=None)
plt.suptitle('Winning vs. Losing Scores')
fig.text(0.5, 0.04, 'Losing Score', ha='center')
fig.text(0.04, 0.5, 'Winning Score', va='center', rotation='vertical')
show_fig('scatter_winscore_by_losescore.png')

scatter_winscore_by_losescore.png

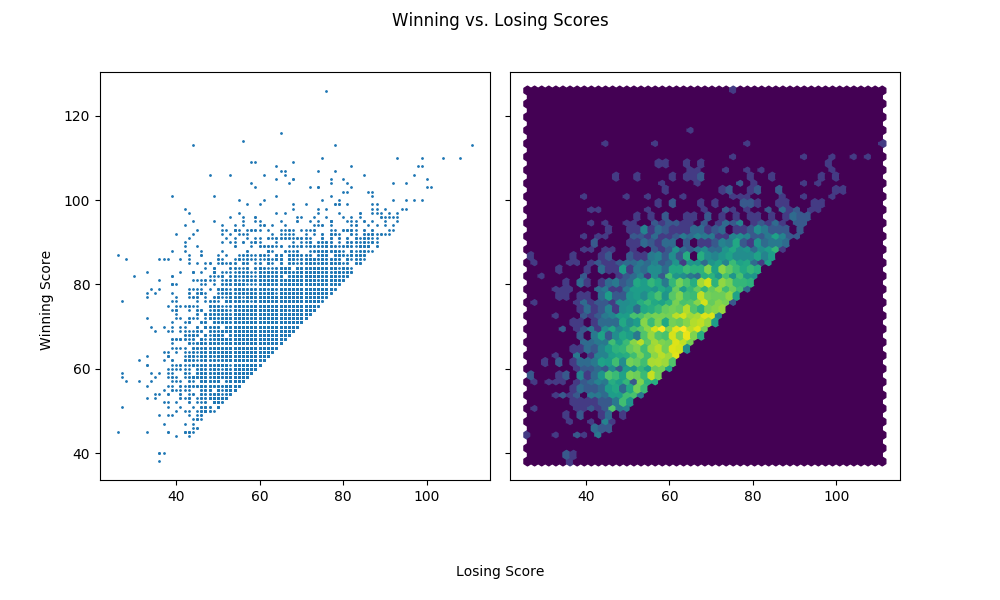
When the losing team scores high, the games are more competitive in a sense that there's less score difference. This is intuitive because there's a soft threshold for the total points scored in a game due to the play-clock.

3.6 Distribution of score difference by losing team's points

fig, axes = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(10, 6))
axes[0].scatter(data['score_l'], data['scorediff'].abs(), s=1)
axes[1].hexbin(data['score_l'], data['scorediff'].abs(), bins='log', gridsize=50)
plt.subplots_adjust(left=0.1, bottom=0.2, right=None, top=None, wspace=0.05, hspace=None)
plt.suptitle('Score Difference vs. Losing Score')
fig.text(0.5, 0.04, 'Losing Team Points', ha='center')
fig.text(0.04, 0.5, 'Score Difference', va='center', rotation='vertical')
show_fig('scatter_scorediff_by_losingpoints.png')

scatter_scorediff_by_losingpoints.png

This plot shows the same information as the previous one.

4 Questions

4.1 How many times does a pair of teams play each other in a season?

num_encounters = data.groupby(['team1', 'team2']).size().value_counts()
print_df(pd.DataFrame({'num_encounters':num_encounters.index,
                       'count': num_encounters,
                       'prop': num_encounters / num_encounters.sum()})
         .set_index('num_encounters'))
num_encounters count prop
1 24640.642839
2 11500.300026
3 2190.0571354

Only about 30% of all pairs play twice in a season. About 5.7% of all pairs play three times.

4.2 Does the outcome of a regular season game between team1 and team2 predict the outcome in the tournament?

tourney_matchups = data.loc[data.tourney == 1]
regular_matchups = data.loc[data.tourney == 0]
joined_matchups = pd.merge(regular_matchups, tourney_matchups, on=['team1', 'team2'], suffixes=('_regular', '_tourney'))
print_df(joined_matchups[['team1', 'team2', 'seednum1_tourney', 'seednum2_tourney', 'team1win_tourney', 'team1win_regular']])
team1 team2 seednum1_tourney seednum2_tourney team1win_tourney team1win_regular
0 1181 1277 1 7 1 1
1 1412 1417 14 11 0 0
2 1181 1458 1 1 1 1
3 1211 1417 2 11 1 1
4 1257 1301 4 8 1 0

In 2015, there's only five regular season games between two teams that played in a tournament game. In four out of five cases, the outcome from the tournament agreed with the outcome from the regular season.